- Teacher: ghali djellouli
I. Rappels généraux sur les nombres :
![]() L’ensemble
L’ensemble ![]() des entiers naturels est fermé sous les lois de l’addition
des entiers naturels est fermé sous les lois de l’addition ![]() . et la multiplication
. et la multiplication ![]() .
.
![]() Et pour pouvoir résoudre pour x toute équation du type :
Et pour pouvoir résoudre pour x toute équation du type : ![]() ; où :
; où : ![]() ; il faut passer aux entiers relatifs
; il faut passer aux entiers relatifs ![]()
![]() Et pour résoudre pour x toute équation de la forme: px + q = 0; pour
Et pour résoudre pour x toute équation de la forme: px + q = 0; pour ![]() ; il faut passer aux nombres rationnels
; il faut passer aux nombres rationnels ![]() pour
pour ![]() ; et
; et ![]() .
.
![]() Ce dernier système est formé de quatre opérations de l’arithmétique mais on ne peut pas résoudre pour x toute équation du type:
Ce dernier système est formé de quatre opérations de l’arithmétique mais on ne peut pas résoudre pour x toute équation du type: ![]() Où
Où ![]() .
.
![]() Les nombres réels
Les nombres réels ![]() permettent de résoudre certaines de ces équations mais pas toutes. Ils forment un système fermé sous les quatre opérations arithmétique qui est de plus complet au sens où toute suite
permettent de résoudre certaines de ces équations mais pas toutes. Ils forment un système fermé sous les quatre opérations arithmétique qui est de plus complet au sens où toute suite ![]() qui satisfait la condition de Cauchy
qui satisfait la condition de Cauchy ![]()
![]() qui est convergente mais on ne peut par exemple obtenir une solution de l’équation
qui est convergente mais on ne peut par exemple obtenir une solution de l’équation ![]() dans
dans![]()
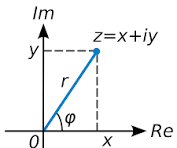
![]() Il faut pour cela construire l’espace des nombres complexes
Il faut pour cela construire l’espace des nombres complexes![]() . Cet ensemble s’écrit sous la forme
. Cet ensemble s’écrit sous la forme
![]()
![]() / Où
/ Où ![]() l’imaginaire
l’imaginaire
Ø L’ensemble des nombres complexes:
o Question: trouver un nombre réel solution de l’équation algébrique ![]()
o Réponse: il n’existe pas de nombre ![]() qui soit solution de l’équation
qui soit solution de l’équation ![]()
⇾ Pour donner des solutions à cette équation et à des équations semblables, on introduit un ensemble plus grand que celui des nombres réels; On appelle cet ensemble les nombres complexes.
Définition: un nombre complexe z s’écrit sous la forme dite algébrique : ![]() où
où ![]() et
et ![]() sont des nombres réels, et
sont des nombres réels, et ![]() est appelé l’unité imaginaire, à la propriété
est appelé l’unité imaginaire, à la propriété ![]() .
.
Ø Le nombre ![]() est appelé la partie réel de
est appelé la partie réel de ![]() on note
on note ![]() ;
;
Ø Le nombre ![]() est appéleé la partie imaginre de
est appéleé la partie imaginre de ![]() on note
on note ![]() ;
;
Ø L’ensemble des nombres complexes est noté ₵.
- Teacher: malika safer
I. Rappels généraux sur les nombres :
![]() L’ensemble
L’ensemble ![]() des entiers naturels est fermé sous les lois de l’addition
des entiers naturels est fermé sous les lois de l’addition ![]() . et la multiplication
. et la multiplication ![]() .
.
![]() Et pour pouvoir résoudre pour x toute équation du type :
Et pour pouvoir résoudre pour x toute équation du type : ![]() ; où :
; où : ![]() ; il faut passer aux entiers relatifs
; il faut passer aux entiers relatifs ![]()
![]() Et pour résoudre pour x toute équation de la forme: px + q = 0; pour
Et pour résoudre pour x toute équation de la forme: px + q = 0; pour ![]() ; il faut passer aux nombres rationnels
; il faut passer aux nombres rationnels ![]() pour
pour ![]() ; et
; et ![]() .
.
![]() Ce dernier système est formé de quatre opérations de l’arithmétique mais on ne peut pas résoudre pour x toute équation du type:
Ce dernier système est formé de quatre opérations de l’arithmétique mais on ne peut pas résoudre pour x toute équation du type: ![]() Où
Où ![]() .
.
![]() Les nombres réels
Les nombres réels ![]() permettent de résoudre certaines de ces équations mais pas toutes. Ils forment un système fermé sous les quatre opérations arithmétique qui est de plus complet au sens où toute suite
permettent de résoudre certaines de ces équations mais pas toutes. Ils forment un système fermé sous les quatre opérations arithmétique qui est de plus complet au sens où toute suite ![]() qui satisfait la condition de Cauchy
qui satisfait la condition de Cauchy ![]()
![]() qui est convergente mais on ne peut par exemple obtenir une solution de l’équation
qui est convergente mais on ne peut par exemple obtenir une solution de l’équation ![]() dans
dans![]()
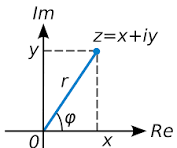
![]() Il faut pour cela construire l’espace des nombres complexes
Il faut pour cela construire l’espace des nombres complexes![]() . Cet ensemble s’écrit sous la forme
. Cet ensemble s’écrit sous la forme
![]()
![]() / Où
/ Où ![]() l’imaginaire
l’imaginaire
Ø L’ensemble des nombres complexes:
o Question: trouver un nombre réel solution de l’équation algébrique ![]()
o Réponse: il n’existe pas de nombre ![]() qui soit solution de l’équation
qui soit solution de l’équation ![]()
⇾ Pour donner des solutions à cette équation et à des équations semblables, on introduit un ensemble plus grand que celui des nombres réels; On appelle cet ensemble les nombres complexes.
Définition: un nombre complexe z s’écrit sous la forme dite algébrique : ![]() où
où ![]() et
et ![]() sont des nombres réels, et
sont des nombres réels, et ![]() est appelé l’unité imaginaire, à la propriété
est appelé l’unité imaginaire, à la propriété ![]() .
.
Ø Le nombre ![]() est appelé la partie réel de
est appelé la partie réel de ![]() on note
on note ![]() ;
;
Ø Le nombre ![]() est appéleé la partie imaginre de
est appéleé la partie imaginre de ![]() on note
on note ![]() ;
;
Ø L’ensemble des nombres complexes est noté ₵.
- Teacher: malika safer
- Teacher: youcef cherchab

Ce plan de cours de thermodynamique vise à décrire la méthodologie d'enseignement de cette matière aux étudiants de Licence 2 en Sciences de la Matière (SM). Il met en avant une approche pédagogique interactive et diversifiée, comprenant des conférences magistrales, des travaux dirigés en petits groupes, des débats et discussions, ainsi que des études de cas. L'objectif principal est de favoriser une compréhension approfondie des concepts de base de la thermodynamique, tout en développant les compétences analytiques et expérimentales des étudiants. Ce plan vise également à promouvoir le travail en équipe, l'esprit critique et la responsabilité professionnelle des apprenants dans l'application des principes thermodynamiques.
- Teacher: semmah abdelwahed
- Teacher: khedidja talbi
- Teacher: khedidja talbi
- Teacher: semmah abdelwahed
